“Why Should I Trust You?”

Abstract

提出了一个可以解释任意分类模型预测结果的方法（局部代理模型）。

Intro

一句话介绍：训练一个基本的可解释模型使其在单个实例邻域附近的预测能力逼近原模型，通过训练这么一个可解释的模型来解释原模型在此实例上的预测。

Core1

$$ \xi(x)=\underset{g \in G}{\operatorname{argmin}} \mathcal{L}\left(f, g, \pi_x\right)+\Omega(g) $$

$$
\mathcal{L}\left(f, g, \pi_x\right)=\sum_{z, z^{\prime} \in \mathcal{Z}} \pi_x(z)\left(f(z)-g\left(z^{\prime}\right)\right)^2
$$

$$
\pi_x(z)=\exp \left(-D(x, z)^2 / \sigma^2\right)
$$

流程：

• 选择想要对其黑盒预测进行解释的感兴趣实例。 x

• 扰动数据集并获得这些新点的黑盒预测。Z

• 根据新样本与目标实例的接近程度对其进行加权。

• 在新数据集上训练加权的，可解释的模型。

• 通过解释局部模型来解释预测。

A. Interpretable Data Representations

可解释的解释方法（interpretable explanation）需要以一种人能理解的表征方式，而不能直接是模型使用的feature。
作者将原数据x映射成interpretable version $x^{\prime}$

e.g. 图像分类中$x^{\prime}$可以是像素块（邻近像素组成的像素块）是否出现的二进制向量
e.g. 文本分类中$x^{\prime}$可以是表示词是否出现的二进制向量

后话：
向量长度也就是特征数K由Lasso算法确定和限制，这影响到解释模型g的复杂程度$\Omega(g)$
这种表征存在解释力不足的情况

B. Fidelity-Interpretability Trade-off

f是待解释的原模型；g是待求解的可解释模型。
用基本的可解释模型g在模型f的局部做逼近，g可以是线性模型、决策树、下降规则集等。
（因为要做到模型无关的可解释，所以不对f做任何假设。
$\pi_x$ 是实例x的邻域，$\Omega(g)$ 是模型g复杂程度的度量（线性模型的非零权重数量、决策树的深度）
则我们的目的：在可理解的前提下尽量减小在由 $\pi_x$ 定义的某一Local field上g与f的差距即$\mathcal{L}$。
$$
\xi(x)=\underset{g \in G}{\operatorname{argmin}} \mathcal{L}\left(f, g, \pi_x\right)+\Omega(g)
$$

we must minimize $\mathcal{L}$ while having $\Omega(g)$ be low enough to be interpretable by humans.

C. Sampling for Local Exploration

通过 $\pi_x$ 的加权得到$\mathcal{L}$，在实例x附近抽样得到z。

抽样方式：均匀随机抽取x中的非零元素（抽样次数也是均匀随机的）
$$
\pi_x(z)=\exp \left(-D(x, z)^2 / \sigma^2\right)
$$

其中D可以是cosine distance for text, L2 distance for images

1
2
3

if kernel is None:
    def kernel(d, kernel_width):
        return np.sqrt(np.exp(-(d ** 2) / kernel_width ** 2))

D. Sparse Linear Explanations

论文中使用线性模型簇作为G。所以有 $g\left(z^{\prime}\right)=w_g \cdot z^{\prime}$

$$
\mathcal{L}\left(f, g, \pi_x\right)=\sum_{z, z^{\prime} \in \mathcal{Z}} \pi_x(z)\left(f(z)-g\left(z^{\prime}\right)\right)^2
$$
为了保证可解释性，需要对可解释表征加以限制K，在文本分类中K即bag of words中words的数量，在图像分类中即超级像素的数量。K由用户设定，论文中为定数。

Ω 的选取导致优化方程难以直接求解，作者使用Lasso（使用正则化路径）选择K个特征，然后最小二乘去让g近似f。

缺陷：

（interpretable representations）可解释表征存在解释力不足的问题，不能解释
（G）基本可解释模型比如线性模型，在原模型即便在局部也完全非线性时就失效了。
解释的不稳定，在模拟环境中两个很接近的点的解释差异很⼤。

Core2

目的：

挑B个单独的实例解释去对模型有个整体的理解，实例们应尽可能地覆盖那些重要的特征，减少冗余。

用一个n*d的explanation matrix W表示对每个实例而言可解释成分的局部重要性。
$I_{j}$表示第j列的可解释成分在解释空间中的整体重要性，在文本应用中$I_j=\sqrt{\sum_{i=1}^n \mathcal{W}{i j}}$，即一列求和。
下图中，$I{2}>I_{1}$是显然的，因为f2被用来解释更多的实例。

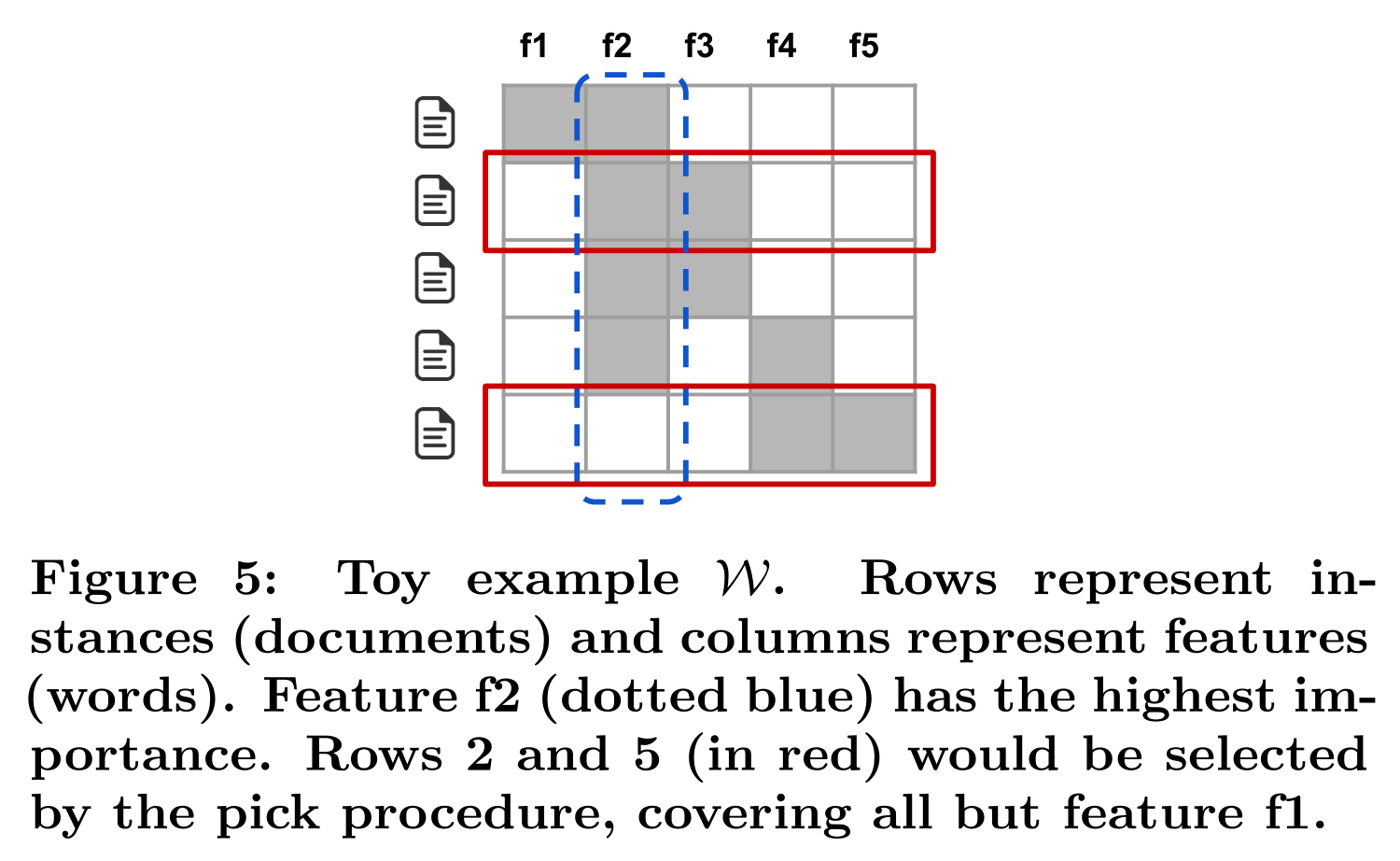
W对重要特征的覆盖率定义为集合函数c：computes the total importance of the features that appear in at least one instance in a set V .
$$
c(V, \mathcal{W}, I)=\sum_{j=1}^{d^{\prime}} \mathbb{1}{\left[\exists i \in V: \mathcal{W}{i j}>0\right]} I_j
$$
去找一个覆盖率最高的实例集合V定义为Pick函数：
$$
\operatorname{Pick}(\mathcal{W}, I)=\underset{V,|V| \leq B}{\operatorname{argmax}} c(V, \mathcal{W}, I)
$$
此最大化加权覆盖函数是个NP-hard问题，所以使用贪心算法求V，即如果增加了实例i导致覆盖率提高，就将其并入V；
$$
V \leftarrow V \cup \operatorname{argmax}_i c(V \cup{i}, \mathcal{W}, I)
$$
SP-LIME算法就可以总结成以下：

WYATT'S CAVE

精读LIME